UVA 10382

UVA 10382 Watering Grass
传送门：洛谷 UVA10382 | UVA 10382 | LibreOJ #10002

题目大意

在一块长 \(L\) 米，宽 \(W\) 米的矩形草坪中共有 \(n\) 个喷水装置，每个喷水装置都在草坪的中心线上（即离两边各 \(\frac{W}{2}\) 米）。
已知：每个喷水装置的位置（即离草坪最左端的距离），以及它能灌溉到的圆形范围的半径。
求问：要确保整块草坪都被灌溉到，则最少需要打开多少个喷水装置？

问题分析

此题为贪心算法中区间覆盖问题的典型例题。

此问题可以转化为：给定多个区间 \([a_i, b_i]\)，选择最少的区间，使它们可以覆盖整个区间 \([1, l]\)。

对于上述问题，可以考虑贪心。将所有区间按照左端点从小到大进行排序。假设 \([0, p)\) 已经被覆盖，对于未被覆盖到的点 \(p(0\le p < l)\)，枚举所有能覆盖到点 \(p\) 的区间，选择其中右端点最大的区间 \([a, b]\)，其中 \(a \le p\)。则覆盖的范围变为了 \([0, b]\)。将 \(p\) 设为 \(b\) 之后的未被覆盖的点（可认为是 \(b\) 本身），继续下次循环。

正确性证明

使用反证法可以证明此贪心解法是最优解。

简单来说，现在区间 \([0, p)\) 均被覆盖，那么对于未被覆盖的点 \(p\)，贪心解法是选择能覆盖点 \(p\) 的所有区间中，右端点最大的区间 \([a_x, b_x]\)。如果选择的区间 \([a_y, b_y]\) 右端点不是最大的，即 \(b_y < b_x\)，那么选择区间 \([a_x, b_x]\) 能够多选择到区间 \((b_y, b_x]\) ，比该方案更优；如果选择不能覆盖点 \(p\) 的区间，那么还需要再增加一个区间来覆盖点 \(p\)。

本题具体解法

计算每个区域的端点

对于在矩形草坪上圆形的覆盖范围，可以将其转化为一维直线（草坪中心线 \(center\)）上的区间覆盖问题。

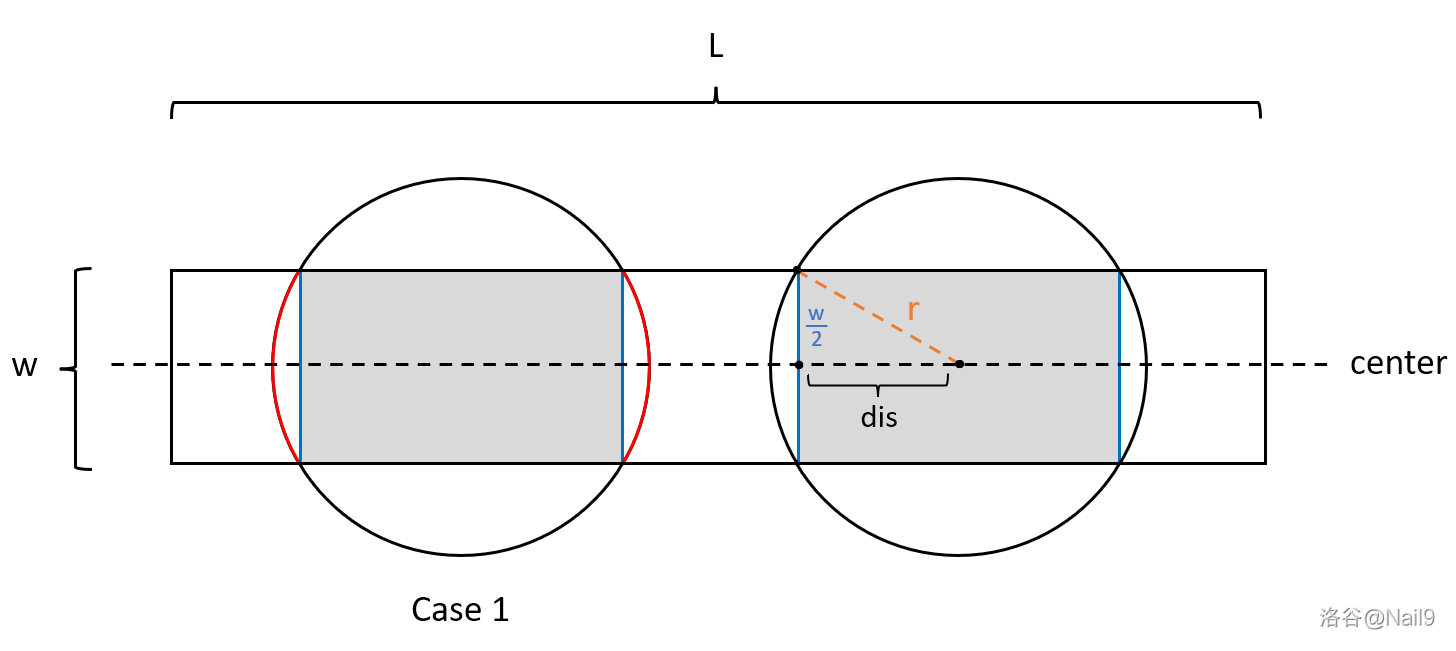
观察到圆形范围在矩形草坪中覆盖的图形有两种情况：当圆形半径 \(r > \frac{W}{2}\) 时，图形为两边有弧度的矩形；当 \(r \le \frac{W}{2}\) 时，图形为完整的圆形（如图灰色部分）。

对于第一种情况，实际起到作用的是下图灰色矩形代表的区间。在读入时可以预处理它的左右两个边界，即蓝色边框的位置。具体地，使用勾股定理计算左右边界：令 \(dis = \sqrt {r^2 - (\frac{w}{2})^2}\)，则左边界为 \(p - dis\)，右边界为 \(p + dis\)，其中 \(p\) 为喷水装置的位置。

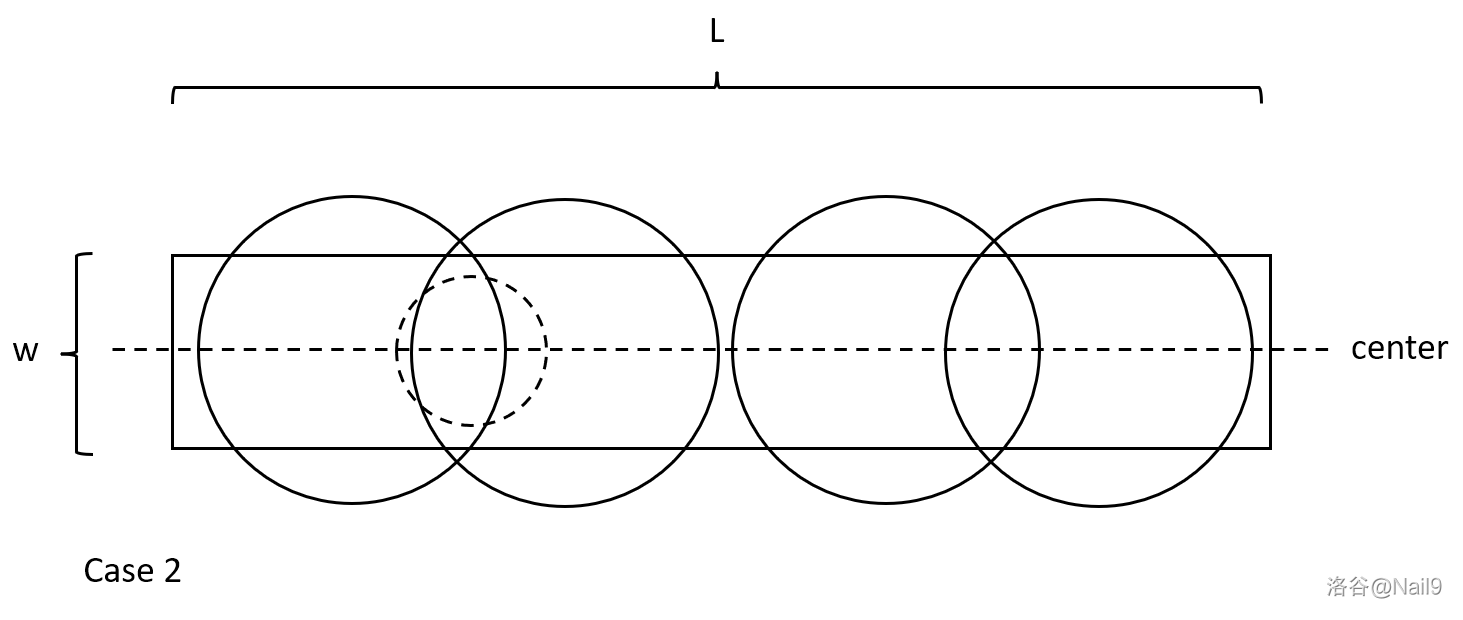
类似地，对于第二种情况，实际并没有起到覆盖面积的作用（如图，这部分图形没有起到任何作用）。在读入 \(r \le \frac{W}{2}\) 时应当忽略该喷水装置。

#define ld long double
typedef pair<ld, ld> pdd;
vector<pdd> d;    // d 数组中存储左右边界

int n = 0, tms, l, w;    // tms, l, w 分别为读入的区间个数、草坪长度、草坪宽度
scanf("%d%d%d", &tms, &l, &w);
for(int i = 1, p, r; i <= tms; i ++) {
    scanf("%d%d", &p, &r);    // p, r 分别为该喷水装置的位置、喷水半径
    if(2 * r <= w) continue;    // 对于第二种情况，直接忽略
    ld dis = sqrt(r * r - w * w / (ld)4.0);    // 对于第一种情况，计算 dis 的值以计算左右边界
    d.push_back({p - dis, p + dis});
    n ++;    // n: d 数组中区间的个数
}

按照左端点排序

按照左端点从小到大的顺序对 \(d\) 数组排序。

bool cmp(const pdd & x, const pdd & y) {    // 当然，pair 类型的排序默认顺序就是先按照第一个元素的大小
    return x.first < y.first;    // first 是左端点的值
}

sort(d.begin(), d.end(), cmp);

贪心选择区间

对于某个未被覆盖到的点 \(p (0\le p < l)\)，枚举所有能覆盖到点 \(p\) 的区间，选择其中右端点最大的喷水装置，并将 \(p\) 更新为右端点的坐标，作为下一个未被覆盖的点，继续循环。
其中，枚举所有能覆盖点 \(p\) 的区间，可以从上一次循环枚举到的最后一个区间之后开始。

对于未被覆盖到的点 \(p\)，如果没有任何区间能够覆盖它，则无法灌溉，输出 \(-1\)。
如果 \(p\) 超过 \(l\)，说明全部覆盖完成，可以输出答案。

bool flg = false;    // 无法灌溉的情况
int ans = 0, x = 0;    // ans: 选择的区间数量, x: 枚举的区间
ld p = 0;    // 所有未被覆盖到的点
while(p < l) {
    ld fp = -1;
    while(x < n && d[x].first <= p) {    // 在 n 个区间中枚举 x，d[x].first<=p 确保区间能够覆盖到点 p
        if(p <= d[x].second)
            fp = max(fp, d[x].second);    // 求所有符合的区间的右端点的最大值
        x ++;
    }
    if(fp == -1) {    // fp 没变过说明没有区间能够覆盖点 p，因此无法灌溉
        flg = true;
        break;
    }
    ans ++;    // 选择了一个喷水装置，答案 + 1
    p = fp;    // 查找下一个未被覆盖的点 p 为之前找到的最大的右端点的值
}
flg ? printf("-1\n") : printf("%d\n", ans);

完整代码

Warning

提交到 UVA 上时，涉及到位置的变量建议都定义为浮点型；

Libre OJ 上需要多读入一行多测数据组数 \(T\)，而 UVA 不需要。

#include <bits/stdc++.h>
#define ld long double
using namespace std;
typedef pair<ld, ld> pdd;
vector<pdd> d;

bool cmp(const pdd & x, const pdd & y) {
    return x.first < y.first;
}

int main() {
    int n, tms;
    ld l, w;
    while(scanf("%d%llf%llf", &tms, &l, &w) == 3) {
        d.clear();
        n = 0;
        for(int i = 1; i <= tms; i ++) {
            ld p, r;
            scanf("%llf%llf", &p, &r);
            if(2 * r <= w) continue;
            ld ll = sqrt(r * r - w * w / (ld)4.0);
            d.push_back({p - ll, p + ll});
            n ++;
        }
        sort(d.begin(), d.end(), cmp);
        bool flg = false;
        int ans = 0, x = 0;
        ld p = 0;
        while(p < l) {
            ld fp = -1;
            while(x < n && d[x].first <= p) {
                if(p <= d[x].second)
                    fp = max(fp, d[x].second + 0.001);
                x ++;
            }
            if(fp == -1) {
                flg = true;
                break;
            }
            ans ++;
            p = fp;
        }
        flg ? printf("-1\n") : printf("%d\n", ans);
    }
    return 0;
}